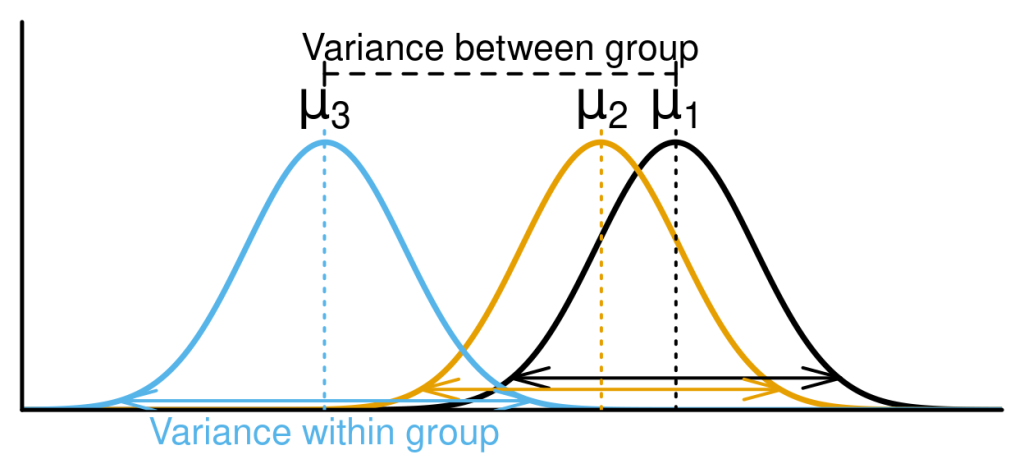
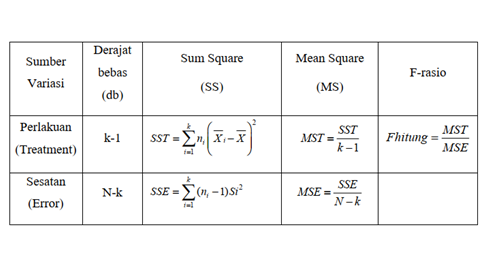
Analysis of Variance (ANOVA) adalah salah satu teknik statistik yang digunakan untuk membandingkan rata-rata dari tiga atau lebih kelompok yang berbeda untuk menentukan apakah terdapat perbedaan signifikan di antara mereka. Metode ini sangat berguna dalam penelitian ilmiah, terutama dalam eksperimen di mana ada perlunya membandingkan efek dari beberapa perlakuan atau faktor.
Anova dapat didefinisikan sebagai teknik statistik yang digunakan untuk menguji perbedaan rata-rata dari dua atau lebih kelompok.
Pengertian Anova Menurut Para Ahli
1. George W. Snedecor (1956):
ANOVA adalah teknik statistik yang digunakan untuk menguji apakah terdapat perbedaan yang signifikan antara dua atau lebih kelompok rata-rata.
2. Montgomery (2009):
ANOVA adalah prosedur statistik yang digunakan untuk membandingkan rata-rata dari dua atau lebih kelompok.
3. Walpole (2007):
ANOVA adalah metode statistik yang digunakan untuk menguji pengaruh satu atau lebih faktor pada variabel dependen.
4. Ghozali (2011):
ANOVA adalah teknik statistik yang digunakan untuk menguji pengaruh satu atau lebih variabel bebas terhadap variabel terikat, dengan asumsi bahwa variabel bebas tersebut bersifat kategorik.
5. Mukjizat (2016):
ANOVA adalah metode statistik yang digunakan untuk menguji perbedaan rata-rata dua atau lebih kelompok, dengan asumsi bahwa data berdistribusi normal dan memiliki varians yang homogen.
Dalam konteks tertentu, beberapa istilah lain terkadang digunakan untuk menggambarkan fungsi serupa yang dilakukan oleh ANOVA. Berikut beberapa diantaranya:
- Uji F: Ini merujuk pada uji statistik yang digunakan dalam ANOVA untuk menguji hipotesis terkait perbedaan antara rata-rata kelompok.
- Analisis varians: Ini adalah terjemahan literal dari ANOVA, namun jarang digunakan sebagai pengganti.
- Tes perbandingan banyak sampel: Ini adalah istilah yang lebih umum yang menggambarkan tujuan ANOVA, yaitu membandingkan rata-rata dari beberapa kelompok sampel.
Bagaimana cara kerja ANOVA?
ANOVA bekerja dengan membandingkan variabilitas antara kelompok dengan variabilitas dalam kelompok. Metode ini menghitung dua jenis variabilitas: variabilitas antar kelompok (disebabkan oleh perbedaan antara kelompok) dan variabilitas dalam kelompok (disebabkan oleh variasi di dalam kelompok itu sendiri).
ANOVA kemudian menggunakan perbandingan antara dua jenis variabilitas ini untuk menentukan apakah perbedaan antara rata-rata kelompok-kelompok tersebut secara signifikan lebih besar daripada variasi yang diharapkan jika hanya terdapat efek acak. Hasilnya adalah uji statistik yang memberikan informasi apakah ada perbedaan signifikan antara setidaknya dua kelompok.
Asumsi-asumsi dalam ANOVA
Secara sederhana, asumsi adalah dugaan sementara yang dianggap sebagai kebenaran oleh seseorang, tetapi belum tentu benar dan perlu pembuktian.
Berikut adalah poin-poin penting tentang asumsi:
- Merupakan anggapan awal: Asumsi dibuat berdasarkan informasi yang ada, pengalaman, atau intuisi, namun belum terbukti kebenarannya.
- Mempengaruhi pemikiran dan tindakan: Asumsi dapat mempengaruhi cara kita berpikir, mengambil keputusan, dan bertindak.
- Penting untuk diidentifikasi: Adalah penting untuk mengenali dan mempertanyakan asumsi kita sendiri, agar tidak menyebabkan kesalahpahaman atau kesalahan dalam bertindak.
- Dapat berbahaya jika tidak dikonfirmasi: Membuat keputusan berdasarkan asumsi yang salah dapat berdampak negatif.
Contoh asumsi
- “Dia pasti terlambat karena macet.”
- “Semua orang yang sukses pasti bekerja keras.”
- “Produk ini pasti bagus karena banyak yang membeli.”
Jenis-jenis asumsi
- Asumsi deskriptif: Menjelaskan sesuatu yang dianggap benar berdasarkan informasi yang ada.
- Asumsi normatif: Menjelaskan bagaimana sesuatu seharusnya terjadi atau dilakukan.
- Asumsi prediksi: Memprediksi bagaimana sesuatu akan terjadi di masa depan.
Ada beberapa asumsi yang perlu dipertimbangkan saat menggunakan ANOVA. Pertama, asumsi tentang distribusi data, yang harus berdistribusi normal di setiap kelompok. Kedua, homogenitas varians, yang berarti variabilitas dalam setiap kelompok harus sekitar sama. Ketiga, independensi, yaitu observasi dalam setiap kelompok harus independen satu sama lain. Pelanggaran asumsi-asumsi ini dapat menghasilkan kesalahan interpretasi dan penarikan kesimpulan yang tidak akurat.
Jenis-jenis ANOVA
Terdapat beberapa jenis ANOVA yang digunakan berdasarkan desain penelitian dan jumlah faktor yang dipertimbangkan. ANOVA satu arah (one-way ANOVA) digunakan ketika hanya satu faktor yang dipertimbangkan. ANOVA dua arah (two-way ANOVA) digunakan ketika ada dua faktor atau lebih yang ingin dianalisis, baik secara bersamaan maupun interaksinya. Selain itu, ada juga MANOVA (Multivariate Analysis of Variance) yang digunakan ketika terdapat lebih dari satu variabel dependen.
Kapan Sebaiknya Menggunakan ANOVA?
ANOVA (Analysis of Variance) adalah teknik statistik yang digunakan untuk membandingkan rata-rata dari dua atau lebih kelompok. Penggunaan ANOVA ideal dalam beberapa situasi berikut:
1. Membandingkan lebih dari dua kelompok
ANOVA unggul dibandingkan uji t-test saat ingin membandingkan rata-rata dari lebih dari dua kelompok. Contohnya, jika ingin membandingkan rata-rata skor tes matematika dari tiga kelompok siswa yang belajar dengan metode belajar yang berbeda, ANOVA adalah pilihan tepat.
2. Menganalisis pengaruh satu atau lebih faktor
ANOVA memungkinkan analisis pengaruh satu atau lebih faktor (variabel independen) terhadap variabel dependen. Contohnya, peneliti dapat menggunakan ANOVA untuk menganalisis pengaruh jenis pupuk (faktor) terhadap hasil panen (variabel dependen).
3. Data berdistribusi normal dan homogen
ANOVA memiliki asumsi bahwa data berdistribusi normal dan memiliki varians yang homogen antar kelompok. Pastikan data Anda memenuhi asumsi ini sebelum menggunakan ANOVA.
4. Ukuran sampel cukup besar
ANOVA membutuhkan ukuran sampel yang cukup besar (umumnya minimal 30 per kelompok) agar hasil yang diperoleh akurat.
Berikut beberapa contoh situasi di mana ANOVA dapat digunakan:
- Membandingkan rata-rata nilai ujian antar kelas.
- Menganalisis pengaruh jenis pupuk terhadap hasil panen.
- Membandingkan efektivitas tiga obat berbeda untuk mengatasi penyakit tertentu.
- Menganalisis pengaruh jenis kelamin dan usia terhadap tingkat pendapatan.
Tips:
- Konsultasikan dengan ahli statistik atau pengajar jika Anda tidak yakin apakah ANOVA tepat untuk penelitian Anda.
- Periksa asumsi ANOVA sebelum menggunakannya.
- Gunakan software statistik yang sesuai untuk melakukan analisis ANOVA.
- Interpretasikan hasil ANOVA dengan hati-hati dan pertimbangkan semua faktor yang terlibat.
Artikel lain Tips Analisis Data Skala Penelitian
Memilih tes ANOVA yang tepat
Memilih tes ANOVA yang tepat sangat penting untuk mendapatkan hasil yang akurat. Hal ini bergantung pada desain penelitian, jumlah faktor yang ingin dianalisis, dan asumsi-asumsi yang terpenuhi. Jika hanya ada satu faktor yang ingin dianalisis, maka one-way ANOVA dapat digunakan.
Namun, jika ada interaksi antara dua faktor, two-way ANOVA lebih sesuai. Selain itu, jika ada lebih dari satu variabel dependen, MANOVA adalah pilihan yang tepat.
Menganalisis hasil ANOVA
Setelah melakukan uji ANOVA, langkah berikutnya adalah menganalisis hasilnya. Hal ini melibatkan memeriksa nilai p-value untuk menentukan apakah perbedaan antara kelompok-kelompok tersebut signifikan atau tidak. Jika nilai p-value kurang dari tingkat signifikansi yang telah ditetapkan (biasanya 0,05), maka terdapat perbedaan yang signifikan antara setidaknya dua kelompok.
Perbedaan ANOVA dan t-test
Perbedaan utama antara ANOVA dan t-test adalah dalam jumlah kelompok yang dibandingkan. T-test digunakan untuk membandingkan rata-rata antara dua kelompok, sedangkan ANOVA (Uji F) digunakan untuk membandingkan rata-rata antara tiga atau lebih kelompok. Jika hanya ada dua kelompok yang ingin dibandingkan, maka t-test lebih sesuai. Namun, jika ada lebih dari dua kelompok, ANOVA adalah pilihan yang tepat.
Uji F dan Uji T: Perbedaan dan Persamaan
Uji F dan uji T adalah dua jenis uji statistik yang umum digunakan dalam penelitian untuk membandingkan dua atau lebih kelompok.
Persamaan:
- Tujuan: Membandingkan rata-rata antar kelompok.
- Asumsi: Data berdistribusi normal dan memiliki varians yang homogen.
Perbedaan:
| Aspek | Uji F | Uji T |
|---|---|---|
| Jumlah kelompok | Digunakan untuk 2 atau lebih kelompok | Digunakan untuk 2 kelompok |
| Jenis variabel | Numerik (interval/rasio) | Numerik (interval/rasio) |
| Statistik uji | F-statistik | t-statistik |
| Distribusi sampling | Distribusi F | Distribusi t |
| Penggunaan: | Uji simultan (menguji pengaruh semua variabel independen secara bersama-sama) | Uji parsial (menguji pengaruh masing-masing variabel independen secara sendiri-sendiri) |
Contoh:
- Uji F: Digunakan untuk menguji apakah terdapat perbedaan rata-rata tinggi badan antara 3 kelompok etnis yang berbeda.
- Uji T: Digunakan untuk menguji apakah terdapat perbedaan rata-rata nilai ujian antara kelompok laki-laki dan perempuan.
Kesimpulan:
Uji F dan uji T adalah dua alat statistik yang penting untuk membandingkan rata-rata antar kelompok. Pemilihan uji yang tepat tergantung pada jumlah kelompok dan tujuan penelitian.
Software untuk ANOVA
Ada berbagai perangkat lunak statistik yang dapat digunakan untuk melakukan analisis ANOVA, termasuk SPSS, R, SAS, dan Minitab. Perangkat lunak ini menyediakan berbagai fitur dan kemampuan untuk menganalisis data dengan ANOVA sesuai dengan kebutuhan pengguna. Pengguna dapat memilih perangkat lunak yang paling sesuai dengan preferensi dan keahlian analisis statistik mereka.
Contoh Penerapan
Misalkan ada sebuah penelitian yang ingin mengevaluasi efek dari tiga jenis pupuk yang berbeda terhadap pertumbuhan tanaman. Penelitian ini membagi tanaman menjadi tiga kelompok yang masing-masing diberi perlakuan dengan pupuk yang berbeda. Setelah beberapa waktu, tinggi tanaman diukur dan dianalisis menggunakan ANOVA untuk melihat apakah ada perbedaan signifikan antara kelompok-kelompok tersebut.
Interpretasi hasil ANOVA
Jika hasil uji ANOVA menunjukkan nilai p-value kurang dari tingkat signifikansi yang telah ditetapkan, maka kita dapat menyimpulkan bahwa terdapat perbedaan signifikan antara setidaknya dua kelompok. Namun, jika nilai p-value lebih besar dari tingkat signifikansi, maka tidak ada cukup bukti untuk menolak hipotesis nol, yang berarti tidak terdapat perbedaan signifikan antara kelompok-kelompok tersebut. Dengan demikian, interpretasi hasil ANOVA sangat penting dalam membuat kesimpulan yang tepat dari analisis statistik ini.
Referensi:
- Snedecor, G. W. (1956). Statistical methods (5th ed.). Ames, IA: Iowa State University Press.
- Montgomery, D. C. (2009). Design and analysis of experiments (8th ed.). Hoboken, NJ: John Wiley & Sons.
- Walpole, R. E., Myers, R. H., & Ye, K. (2007). Probability and statistics for engineers and scientists (9th ed.). New York: Pearson Education.
- Ghozali, I. (2011). Aplikasi analisis multivariate dengan SPSS (7th ed.). Semarang: Badan Penerbit Universitas Diponegoro.
- Mukjizat, M. (2016). Statistika untuk penelitian (2nd ed.). Yogyakarta: Pustaka Pelajar.
Artikel ini terakhir diperbarui pada: 4 Maret 2024 untuk menjaga relevansi dengan kondisi terkini.